算法基础-前缀和

前缀和

一、什么是前缀和？

一维前缀和：

有一个一维数组 和该数组的一维前缀和数组 ，则 和 满足以下关系：

二维前缀和：

有一个二维数组 和该数组的二维前缀和数组 （其同样是个二维数组），则 和 满足以下关系：

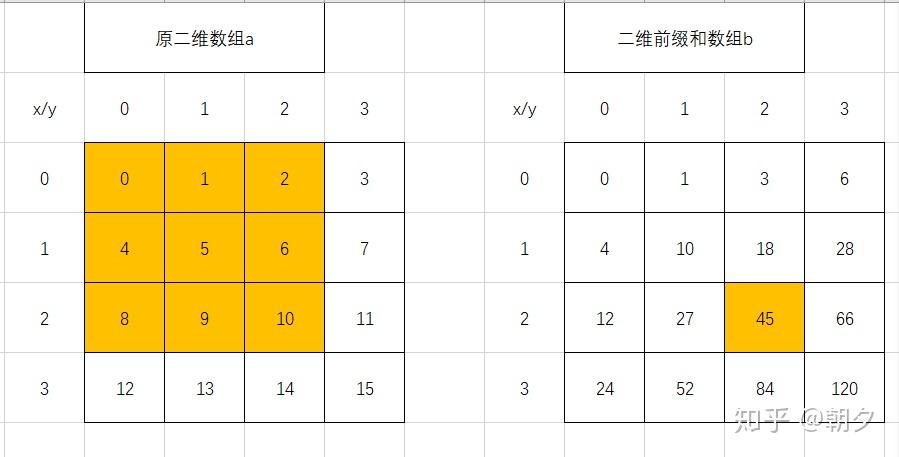
看公式可能有点懵，看底下的图更好理解。

右侧标注橙色的二维前缀和元素，其值是左侧的原二维数组中标注橙色的所有元素的和。

二、如何得到前缀和？

一维前缀和：

很容易就可以发现：

代码实现如下：

for(int i=0;i<n;i++)
{
    if(i==0) y[i]=x[i];
    else y[i]=y[i-1]+x[i];
}

二维前缀和：

二维前缀和实际上就是一个矩阵内值的和，而矩阵又可以由两个行数或列数少一的子矩阵组合后，删去重合部分再加上右下角的值来构成，也就是以下式子：

代码实现如下：

for(int y=0;y<n;y++)//n行
    for(int x=0;x<m;x++)//m列
    {
        if(x==0&&y==0) b[y][x]=a[y][x];//左上角的值
        else if(x==0) b[y][x]=b[y-1][x]+a[y][x];//第一列
        else if(y==0) b[y][x]=b[y][x-1]+a[y][x];//第一行
        else b[y][x]=b[y-1][x]+b[y][x-1]-b[y-1][x-1]+a[y][x];
    }

三、前缀和有什么用？

3.1 说明

前缀和是一种预处理，用于降低查询时的时间复杂度。

举个例子：给定 个整数，然后进行 次询问，每次询问求一个区间内值的和。

如果用暴力写法，那每次询问都需要从区间左端点循环到区间右端点求和，时间复杂度较大。

这种时候就可以预先求出该数组的一维前缀和。

则 ，其中 和 是给定的区间。每次询问可直接输出答案，这样时间复杂度就降到了 。

3.2 一些前缀和例题

3.2.1 成绩百分比 改编自网易笔试题

班级中共有 位同学，其编号为1~ 。考试中每位同学都取得了一定的成绩。
接下来进行 次询问，每次询问给出一位同学的编号，求这位同学的成绩在班级中的百分比。
百分比求法：不超过这位同学成绩的班级人数（包括这位同学）/总人数×100%。
( ，成绩 )。

解法①暴力解法：

每次询问都遍历所有同学，时间复杂度 ，数据给的很大，必炸。

解法②排序+二分查询：

开一个新的数组，将班级内所有同学的成绩进行排序。每次查询时，先将这位同学的成绩取出，然后通过二分法在已排序的数组中寻找位次并输出。

时间复杂度 ， 是排序的复杂度， 是 次查询的复杂度。

能过，但不是最佳解法。

解法③前缀和：

根据题意可以发现，由于成绩分数都小于等于150，所以桶排序可以上场了。

先通过桶排序得到考到每个分数的人数。

接下来通过前缀和来计算不超过该分数的人数，式子如下：

，其中 表示分数， 表示考到该分数的人数。

这样查询时的时间复杂度就变成了 。

3.2.2 数列找不同 洛谷 P3901

这题准确来说是维护前缀最大值，但思想是一样的。

只需要 的处理，就能达成 的查询，否则这题则需要莫队算法。

3.2.3 在你窗外闪耀的星星 洛谷 P3353

这题的题目描述……有点杀单身狗。

不过这题真的不需要用线段树，配合前缀和即可写了。